数据结构 | 通用树

一些术语：

通用树（以下简称树）-由一个或一个以上结点组成的有限集，其中没有父结点的结点称为根结点。
最左子结点-子树从左到右排列，其中最左边的子树的根结点称为最左子结点。
（结点M的）出度-（结点M的）子结点数目。
森林-一棵或更多棵树的集合。

注意到树和二叉树的主要区别：

二叉树的出度至多为2，但树没有限制；
二叉树交换左右子结点得到的新树与原树不同，但树交换没有区别。

一　树结点的ADT

注意到树的出度是没有限制的，那么建立树类时就应该注意找到一种能够处理这种情况的方法。实现它一般来说可以采用数组或链表的形式，后者更为常见。

单击此处查看树和树结点的类定义

下面是从教材中摘录的树和树结点的类定义。注意到其中的leftmostChild和rightSibling函数，使用它们可以很好的完成遍历操作。

// General tree node ADT
template <typename E> class GTNode {
public:
  E value();                    // Return node's value
  bool isLeaf();                // True if node is a leaf
  GTNode* parent();             // Return parent
  GTNode* leftmostChild();      // Return first child
  GTNode* rightSibling();       // Return right sibling
  void setValue(E&);            // Set node's value
  void insertFirst(GTNode<E>*); // Insert first child
  void insertNext(GTNode<E>*);  // Insert next sibling
  void removeFirst();           // Remove first child
  void removeNext();            // Remove next sibling
};

// General tree ADT
template <typename E> class GenTree {
public:
  void clear();                               // Send all nodes to free store
  GTNode<E>* root();                          // Return the root of the tree
  // Combine two subtrees
  void newroot(E&, GTNode<E>*, GTNode<E>*);
  void print();                               // Print a tree
}

这就是一种用链表的形式实现的树和树结点的类。

二　树的遍历

树的遍历与二叉树类似，分为前根遍历、中根遍历、后根遍历。其中中根遍历因为子结点数目不确定的原因而难以定义，一般也不使用。
遍历过程会使用到上面的leftmostChild和rightSibling函数，每当遍历子结点时，总是先调用leftmostChild函数访问最左子结点，然后对其调用rightSibling函数来依次访问最左子结点右边的兄弟结点，直到最右子结点（它右边的兄弟结点是NULL）。

三　父指针表示法

在解决“任意给出两个不同的结点，判断它们是否在同一棵树中”这样的问题时，仅凭上文的方法是无法解决的。一个有效的解决方法是使用父指针表示法——只需要顺着父指针链就能追溯到根结点，从而判断给定结点是否在同一棵树中。使用这种方法，每个结点只需要保存一个指针域指向其父结点。

一些术语：

不相交子集-交集为空的两个集合。对于这样的集合，希望提供判断两个结点是否在同一集合中和归并两个集合的操作。
并查算法（也称并查集）-通过合并两个不相交子集来找出两个结点是否在同一个集合的过程。

并查算法用一棵树表示一个集合。结点通常存储在数组中——每个数组元素表示一个结点，并存储该结点的值、父指针（用于区分不同的树）和指向子树的指针（如果有），这样便通过一个数组表示了一组树结构。这一节仅仅将目光聚焦在父指针上。

单击此处查看并查算法的实现

下面是从教材中摘录的并查算法的实现。注意到其中的UNION函数执行归并操作。

// General tree representation for UNION/FIND
class ParPtrTree {
private:
  int* array;           // Node array
  int size;             // Size of node array
  int FIND(int) const;  // Find root
public:
  ParPtrTree(int);                    // Constructor
  ~ParPtrTree() { delete [] array; }  // Destructor
  void UNION(int, int);               // Merge equivalences
  bool differ(int, int);              // True if not in same tree
};

int ParPtrTree::FIND(int curr) const { // Find root
  while (array[curr] != ROOT) curr = array[curr];
  return curr;  // At root
}

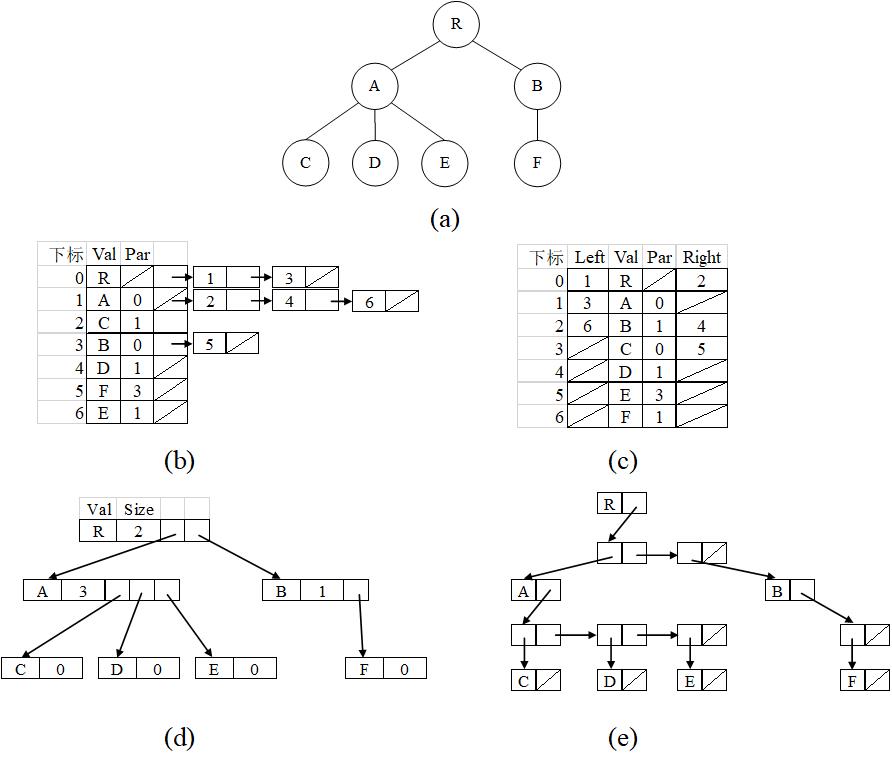
图F1进一步形象地展示了父结点表示法，在这个数组中容纳了两棵树（实际上，对于有n个结点的集合，它对应的数组可以容纳至多n棵无关的树）。为了简明起见，父指针表示为父结点在数组中位置的下标值。树的根结点存储ROOT值，在图F1中表示为斜线。
F1.父指针数组表示法

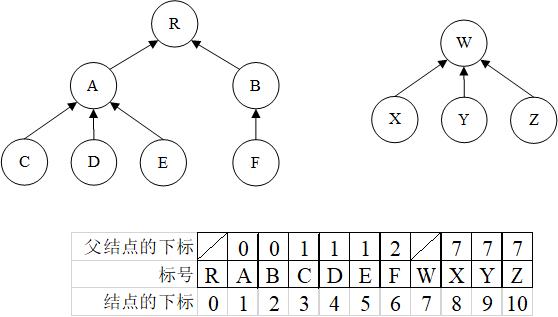
父指针表示法并非是出于一般性目的的，它总是用来解决一些特定的问题，例如在本节开头提到的“任意给出两个不同的结点，判断它们是否在同一棵树中”。上面的实现中已经大致阐述了这个问题的解决思路及其核心算法——并查算法。在这个卡片中，我们要指出这个问题的一个重要应用——解决等价类问题。

以下给出了一些重要的术语阐释以便在后面的阅读中查阅：

等价关系-具有自反性、对称性和传递性的一种关系；
等价类-利用等价关系对一个集合进行划分的结果；
等价对（的表示）-如果图中某两个结点X，Y之间存在一条通路，就认为这两个结点是等价的，并将等价对表示为(X, Y)。如图F2所示，(A, B) (A, C)等等都是等价对；

F2.图示例

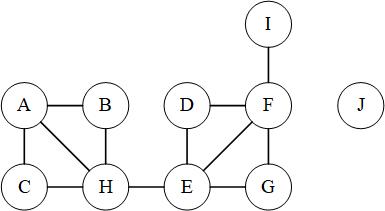
以图F2为例，我们来尝试解决一个等价类问题：已知若干对等价对（如图F2所示），试将其划分为等价类。

这个问题的解决步骤是这样的：

将每一个结点独立（如图F3.a所示）；
输入一个等价关系（从结果而言，等价关系的输入顺序无关紧要，但是会影响问题处理效率，这里忽略顺序对效率的影响），并使用differ函数检查它们是否在同一等价类（即同一棵树）中。如果是，则不做处理；如果不是，则使用UNION函数归并两个等价类。为了使等价对的处理尽可能高效，每个结点到其相应根结点的距离应该尽可能小，因此，在归并前可以采用路径压缩、在归并时可以采用加权合并规则来减少树的高度。

路径压缩
设根结点为R，则路径压缩把由X到R的路径上每个结点的父指针都设置为直接指向R。路径压缩的代价非常接近常数，约为 $\Theta(n \log * n)$ （其中 $\log * n$ 是指在 $n \geq 1$ 之前要对 $n$ 取对数操作的次数）。因此， $n$ 个路径压缩的代价非常接近于 $\Theta(n)$ 。

加权合并规则
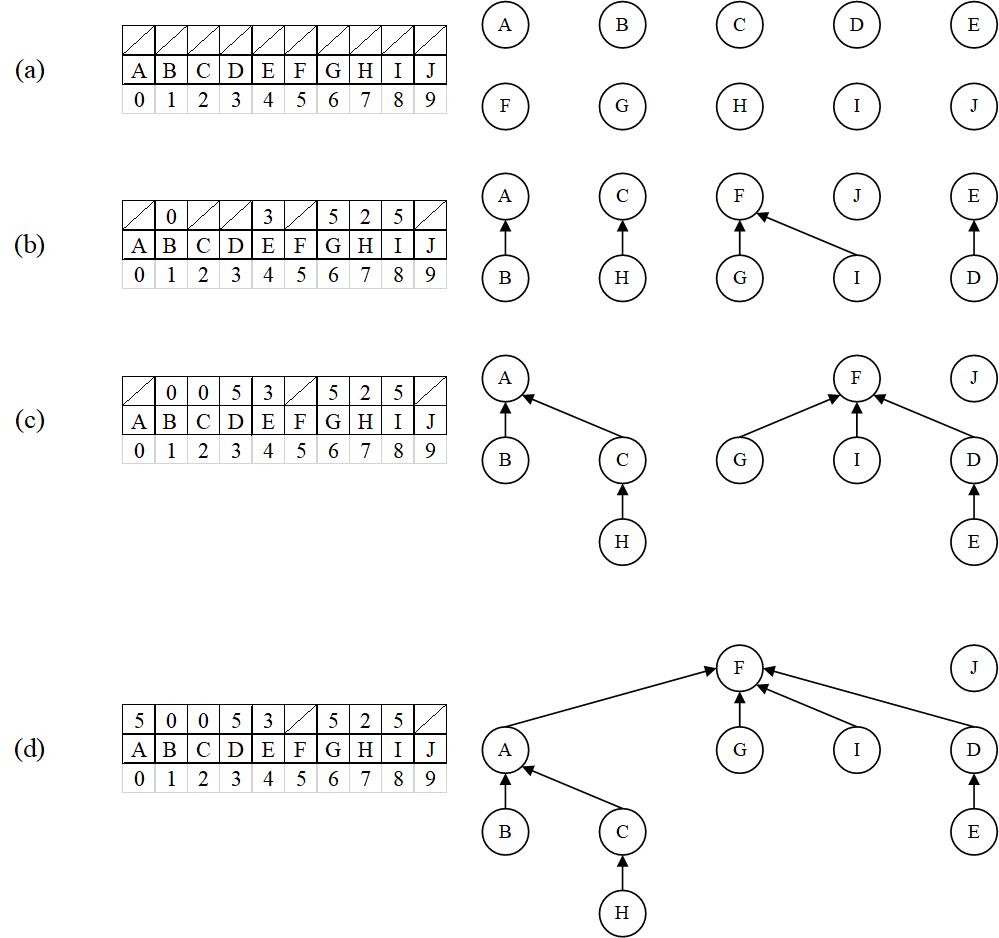
在把结点较少的一棵树与结点较多的一棵树归并时，把结点较少树的根结点指向结点较多树的根结点。这样可以把树的整体深度限制在 $O(\log n)$ 。在图F3.c仅仅运用本方法，在其状态下对等价对(H,E)进行处理，处理结果如图F3.d所示。

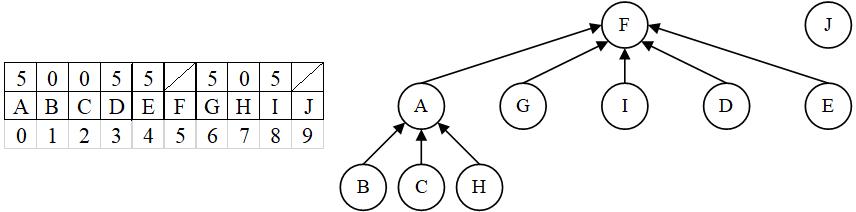
应用以上两种方法，在图F3.c的状态下对等价对(H,E)进行处理，处理结果如图F4所示。其过程如下：

应用路径压缩，在归并前使H指向A、E指向F；
应用加权合并规则，在归并时使A指向F。

F3.等价类问题处理示例
F4.加权合并规则和路径压缩的应用示例

四　树的实现

（一）子结点表表示法

子结点表表示法中，每个分支结点都存储其子结点形成的一个链表。在数组中，每个结点包括结点值，一个父指针（或索引）以及一个指向子结点链表的指针，链表中子结点的顺序从左到右，如图F5.b所示。注意到这种表示法是否能够很好的实现“树和树结点的类定义”抽象数据类型。在实现rightSibling时，本表示法显得过于繁琐。考虑这种情况——如果有一个结点M，并且其父结点为P，那么查找M的兄弟结点就需要沿着结点P的子结点表向右移动，直至找到M，那么其下一个结点就是M的兄弟结点。这个过程较为复杂，最差情况下需要查找全部子结点。

（二）左子结点/右兄弟结点表示法

针对子结点表表示法的缺陷，本表示法进行了改进。在数组中，每个结点包括结点值和指向父结点、最左子结点、右兄弟结点的指针，如图F5.c所示。这样一来，调用rightSibling时只需要读取结点中的右兄弟结点指针即可。更好的是，在子结点表表示法中，对每个结点分配的空间并不是固定的，而这种方法也很好的解决了此问题。

（三）动态结点表示法

除了使用数组来存储结点，类比二叉树，还可以使用指针来实现树。可以为每个结点分配可变的存储空间（它的可变性体现在对于每一结点，其子结点数目可以不同，该性质的强调是为了与二叉树区分开来，因为二叉树的子结点指针数目总是2），有以下三种方式，：

将指向子结点的指针数组作为结点的一部分分配给该结点。这是一种直接的方式，即直接为每个结点分配对应数目的子结点指针数组。这样的方法在子结点数目已知和不变时效果最佳。
使用一系列可利用空间，每一个可利用空间都对应每一个结点的子结点数组大小，如图F5.d所示。当某一结点的子结点数目从M变为N时，从可利用空间取出空间为N的链表，然后空间为M的链表返回可利用空间。
每个结点都存储一条子结点指针链表。如图F5.e所示。

这三种方式的不同之处在于对子结点的处理。第一种方式处理子结点数目不变的情况，第二种方式处理子结点数目变化的情况（注意到这种方式需要提前准备若干不同空间大小的链表），第三种方式的处理更加灵活，它将第二种方式的缺点进行弥补，使得子结点不必再组织在数组中而割裂开来，但它需要更多的空间。

（四）动态结点左子结点/右兄弟结点表示法

本表示法是对动态结点表示法第三种方式的改进，提高了空间效率。在这个方法中，每个结点包括结点值和指向最左子结点、右兄弟结点的指针，它本质上是将树转化为二叉树，“左子结点”是最左子结点，“右子结点”是右兄弟结点。
F5.树的实现示例

五　顺序表示法

树的顺序表示法也是一种树的实现，但与前面树的实现方法有着本质上的区别。它的目的是存储结点的值，其中包含了尽可能少、但对于重建树结构必不可少的信息。因此，这种表示法适合用于将树结构压缩在磁盘上，以备以后使用时重建；也可以用来序列化树结构（序列化是指把一个对象以一系列字节形式存储的过程，以便这种数据结构在计算机之间传输）。
在研究树的顺序表示法前，不妨从二叉树开始探究。

（一）二叉树的顺序表示法

对二叉树而言，每一个结点或者是叶结点，或者是具有两个子结点（其一可能为空）的分支结点。那么应注重对叶结点和分支结点的区分，以及对空结点的表达。方法如下：

区分叶结点和分支结点：采用位向量表示法标记。例如1表示分支结点，0表示树结点。
空结点的表达：使用某一标记，例如/。

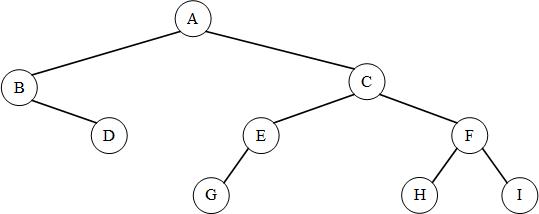
比如对于图F6而言，顺序表示法的结果是AB/DCEG/FHI（位向量是11001100100）。
F6.二叉树的顺序表示法示例

（二）树的顺序表示法

注意到树和二叉树的主要区别（见本文开头），我们需要解决如何表达子结点数目信息的问题，同时不必关注空结点（因为树不存在空结点的定义）。一种有效的方式是直接使用某个标记表示子结点表的结束，例如)，这样就不必再标记叶结点或分支结点了——所有叶结点后都有该标记，因为叶结点没有子结点。比如对图F5.a的树，其顺序表示法的结果是RAC)D)E))BF)))。但是这种方法不能使用在二叉树上，因为二叉树需要区分左右子结点。如果使用此法，譬如对图F6的二叉树而言，将无法区分D是B的左子结点还是右子结点。