一　递归的含义及其两个必要条件

（一）递归的含义

  递归，是指一种通过重复将问题分解为同类的子问题而解决问题的方法。它将大事化小，能够大大减少程序的代码量。

（二）递归的两个必要条件

  1. 存在限制条件，当满足这个限制条件的时候，递归便不再继续；
  2. 每次递归调用之后越来越接近这个限制条件。

二　汉诺塔问题

（一）问题内容

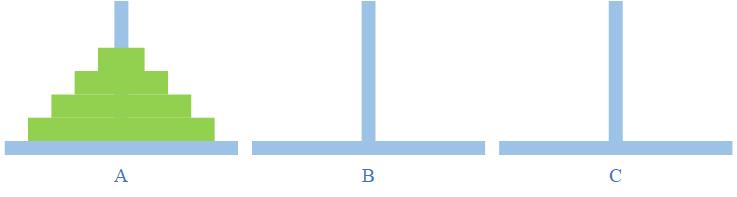
  • BASE-在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置若干个金盘。（如图F1所示）
  • GOAL-把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。
  • RULE-每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

F1.汉诺塔问题

（二）解决思路

  为了满足大盘在下，小盘在上的规则，当金盘进入C杆时，其顺序也应当是先大盘，后小盘。以4个金盘为例，不妨基于C杆考察此问题：
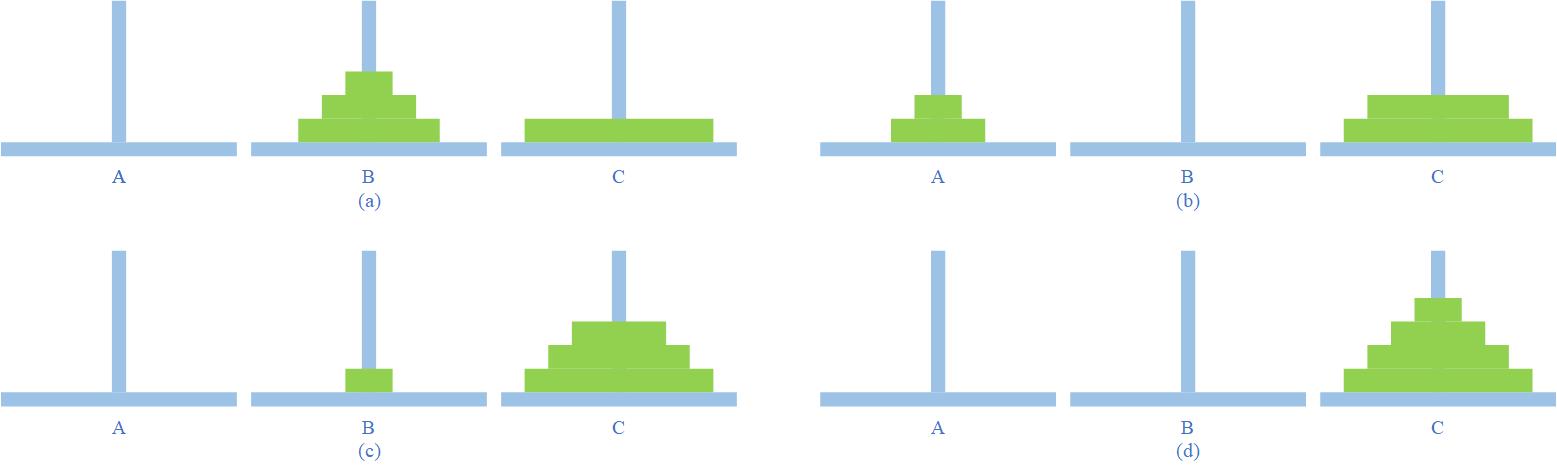
  第1轮转移 当第一个金盘进入C杆时，其余盘应按照从小到大置于B杆；（如图F2.a所示）
  第2轮转移 当第二个金盘进入C杆时，其余盘应按照从小到大置于A杆；（如图F2.b所示）
  第3轮转移 当第三个金盘进入C杆时，其余盘应按照从小到大置于B杆；（如图F2.c所示）
  第4轮转移 当第四个金盘进入C杆时，达到目标。（如图F2.d所示）
F2.汉诺塔问题
  注意到，总是需要将A杆（或B杆）上的n个金盘中的n-1个转移到B杆（或A杆），然后将第n个金盘转移到C杆。并且在转移n-1个金盘的过程中，也同样遵循上述规律，即将A杆（或B杆）上的n-1个金盘中的n-2个转移到C杆，然后将第n-1金盘转移到B杆（或A杆）。这样一来，不难发现该问题可以分解为同类的子类问题，并且符合递归的必要条件——其限制条件是转移前A杆和B杆的金盘数目都为0；并且每轮结束时，金盘数目都减1，越来越接近限制条件。
  基于以上思路进行程序设计。

（三）解决办法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//函数的传入参数n是A杆放置的金盘数目。
int TOH(int n)
{
	//定义返回结果为操作次数。
	static int ret = 0;
	//1.递归限制条件：
	if (n == 0)
		return 0;
	//2.递归部分：
	else
	{
		//2.1.将A杆（或B杆）最底盘之上的n-1个盘子移动至B杆（或A杆）上。
		ret += TOH(n - 1);
		//2.2.将最底盘移动至C杆上。
		ret += 1;
		return ret;
	}
}

三　青蛙跳台阶问题

（一）问题内容

  • BASE-有一只青蛙处于若干阶台阶底层。
  • GOAL-青蛙恰好到达台阶顶层。
  • RULE-青蛙每次跳跃的台阶数仅能为1或2。

（二）解决思路

  注意到青蛙每次跳跃的台阶数仅能为1或2，设跳跃的次数为M，台阶数为N，那么当进行第M次跳跃时，也仅能跳跃1阶或2阶；当进行第M-1次跳跃时，已经跳跃的台阶数是N-1或N-2。类似地，当进行第M-2次跳跃时，已经跳跃的台阶数是N-1-1或N-1-2或N-2-1或N-2-2。据此就可以知道，跳跃N(N≥3)阶台阶的跳法总是跳跃N-1阶台阶的跳法与跳跃N-2阶台阶的跳法之和：

  • 当N=1时，仅有1种跳法；
  • 当N=2时，仅有2种跳法。

  这便符合了递归的必要条件——其限制条件是跳跃前剩余台阶数为1或2；并且每次跳跃结束时，台阶数目都减1或减2，越来越接近限制条件。
  基于以上思路进行程序设计。

（三）解决办法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//函数的传入参数n是台阶数目。
int CS(int n)
{
	//定义返回结果为跳法数目。
	static int ret = 0;
	//1.递归限制条件：
	//1.1.台阶数为1时，有1种跳法。
	if (n == 1)
	{
		return 1;
	}
	//1.2.台阶数为2时，有2种跳法。
	else if (n == 2)
	{
		return 2;
	}
	//2.递归部分：
	else
	{
		//跳跃n阶台阶的跳法总是跳跃n-1阶台阶的跳法与跳跃n-2阶台阶的跳法之和。
		ret = CS(n - 1) + CS(n - 2);
		return ret;
	}
}