算法分析 | 渐进算法分析

快速索引：

化简法则

一运行时间代价

一些术语：

规模-一般指输入量的数目。
算法代价-指一种算法（或者是实现该算法的一个程序实例）所花费的时间（称为时间代价），以及一种数据结构所占用的空间（称为空间代价）。
基本操作-必须具备这样的性质：完成该操作所需时间与操作的数目的具体取值无关。例如在大多数高级语言中两个整数的相加；而 $n$ 个整数的累加便不是基本操作，因为这个操作的时间代价与 $n$ 的大小有关。

运行速度通常是算法代价的关键方面（但注意运行速度绝非等价于算法代价），因此，算法的性能可以以处理一定规模的输入时该算法所需执行的基本操作的数目作为衡量标准。如果我们要观察算法在不同规模输入的情况下的性能，就可以考虑使用函数 $T(n)$ （总是假设 $T(n)$ 非负）来描述它。例如对于一个变量sum，如果忽略与输入规模无关的部分所消耗的时间（比如变量初始化、循环调节变量的增值等），那么有（以下表达式中 $c$ 为常数）：

示例一 将一个整数与变量sum相加：

$T(n)=c$

注：这是一种基本操作，其时间代价总是与规模无关，此时称之为常数运行时间。
示例二 将 $n$ 个整数依次与变量sum相加：

$T(n)=cn$
示例三 将 $n$ 个整数依次与变量sum相加，并将上述过程重复 $n$ 次：

$T(n)=cn^2$

二增长率

根据教材的定义，算法的增长率是指当输入的规模增大时，算法代价的增长速率。

博主认为这样的定义是有歧义的。速率一词常见于运动学中，表示运动的快慢，被定义为路程变化量和时间变化量的比值，即

$v = \frac{\Delta s}{\Delta t}$

类似地，如果按照速率的定义，则这里算法的增长率被定义为算法代价的变化量和输入规模变化量的比值，即

$r = \frac{\Delta T}{\Delta n}$

但是在普遍的定义中，增长率被定义为某一指标的变化量和原来指标的比值，即

$r = \frac{\Delta T}{T_0}$

后者定义更加契合它的内涵。例如在以下博文中，可以发现

在定义线性、二次、指数增长率时，它们所对应的运行时间函数 $T(n)$ 也是线性、二次、指数的。这意味着从运行时间函数计算增长率的过程中并不降阶；但是如果按照前者定义，则等价于对运行时间函数求导，致使增长率比运行时间函数低阶，这导致矛盾。
在算法的上限、下限的阐述中，运行时间的上/下限和增长率的上/下限这两种说法总是可以交换的，这意味着这二者的最高阶总是一致的（渐进分析忽略了常系数和低阶项），应用前者定义也会产生矛盾。

因此在理解时应当采用后者定义。
注：限于博主的认知，以上论断可能有误。如果您发现了不当之处，还望在评论区提出您的想法。

对 $T(n)=cn$ （ $c$ 为常数）的增长率，称之为线性增长率或者线性时间代价；
对 $T(n)$ 中含有形如 $n^2$ 的高次项的增长率，称之为二次增长率；
对 $T(n)=a^n$ （ $a$ 为常数且 $a>0$ ）或 $T(n)=n!$ 的增长率，称之为指数增长率。

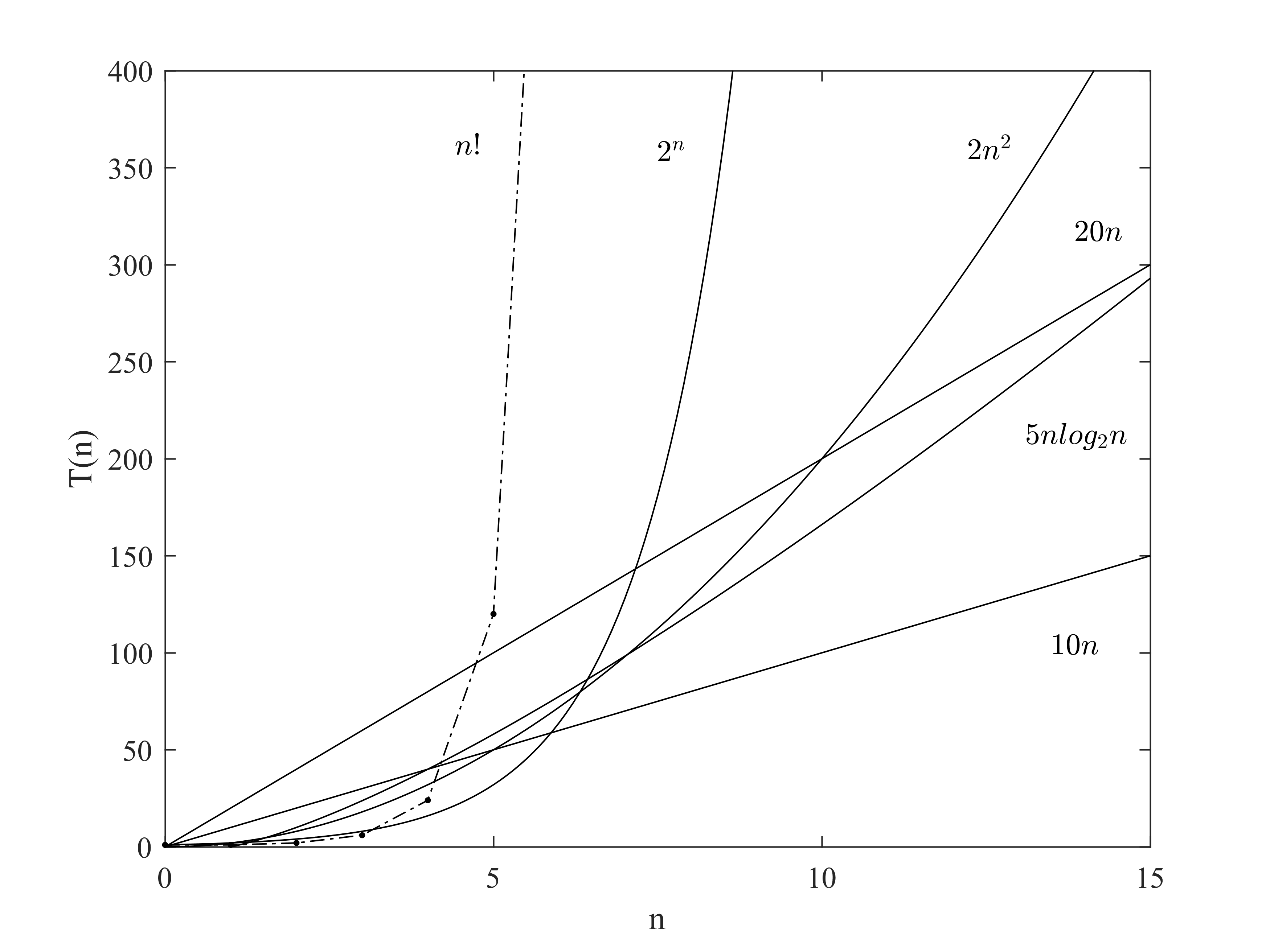
图 $F1$ 作出了这三类运行时间函数的图像示例，并可以得到以下结论（当规模较大时）：

$n^a$ 的增长率总是快于 $\log ^bn$ 和 $\log n^b$ （ $a,b>1$ ）；
$a^n$ 的增长率总是快于 $n^b$ （ $a,b \geq 1$ ）。

实际上，按照增长速率又快到慢总是有（当规模较大时）：阶乘函数、指数函数、幂函数、 $n\log n$ 、线性函数、对数函数、常函数。注意到总是在强调当规模较大时，这实际上运用了一些渐进分析（将会在后文介绍到）的思想。
F1.运行时间函数示例

三最佳、最差和平均情况

即便规模相同，算法的时间代价也可能会因为输入数据不同而不同。算法的最佳情况是指运行时间最短的情形；最差情况是指运行时间最长的情形；平均情况则是分析所有情况下运行时间的平均值。具体考虑哪一种情况依据实际问题和需求确定。实际上，由于最佳情况过于乐观，一般情况并不采用；在实时系统中，比较关注最差情况算法分析；其他情况下则通常考虑平均情况（但需要知道输入数据的分布，否则就只能求助于最差情况分析）。

四渐进分析

在输入规模趋近极限的情况下估算增长率时通常会忽略其常数系数。这样的简化分析方式就是渐进算法分析，常用于算法比较。

（一）上限——“大欧”表示法

上限的定义是：

对于非负函数 $T(n)$ ，如果存在两个正常数 $c$ 和 $c_0$ ，对任意 $n>n_0$ ，满足

$T(n) \leq cf(n)$

则称 $T(n)$ 在集合 $O(f(n))$ 中。

例如对 $T(n)=c_1n^2+c_2n+c_3$ （ $c_1$ 、 $c_2$ 、 $c_3$ 均为常数，平均情况下）：
取 $n_0=1$ （实际上一般情况下 $n_0$ 都比较小，取使不等式成立的最小值），那么当 $n_0>1$ 时，由

$T(n)=c_1n^2+c_2n+c_3 \leq (c_1+c_2+c_3)n^2$

分析得知，当取 $c=c_1+c_2+c_3$ ， $n_0=1$ 时， $T(n) \leq cn^2$ 成立，则称 $T(n)$ 在集合 $O(n^2)$ 中。

特别地，对 $T(n)=c$ （ $c$ 为常数），称 $T(n)$ 在集合 $O(1)$ 中。

注意到在定义中， $O(f(n))$ 是一个集合，它包含了与 $f(n)$ 同阶和比 $f(n)$ 高阶的函数，这意味着上限不止一个。例如，对 $T(n)=c_1n^2+c_2n+c_3$ （ $c_1$ 、 $c_2$ 、 $c_3$ 均为常数，平均情况下）而言，我们知道这个 $T(n)$ 在集合 $O(n^2)$ 中，并且不难证明 $T(n)$ 在集合 $O(n^3)$ 甚至更高阶的集合中。为了更加精确地描述，应当试图寻找最小的上限，例如上例中， $T(n)$ 在集合 $O(n^2)$ 中是更好的说法。

某一种算法的时间代价函数都具有一定的背景——最佳、最差和平均情况。因此在描述上限（或下限）时，同样应当表明它隶属于哪一种情况。因此，例如对上例而言，应当说这种算法在平均情况下的增长率上限是 $\textbf{n}^\textbf{2}$ 。

（二）下限——“大欧米伽”表示法

下限的定义是：

对于非负函数 $T(n)$ ，如果存在两个正常数 $c$ 和 $c_0$ ，对任意 $n>n_0$ ，满足

$T(n) \geq cg(n)$

则称 $T(n)$ 在集合 $\Omega(g(n))$ 中。

$T(n)=c_1n^2+c_2n+c_3 \geq c_1n^2$

分析得知，当取 $c=c_1$ ， $n_0=1$ 时， $T(n) \geq cn^2$ 成立，则称 $T(n)$ 在集合 $\Omega(n^2)$ 中。

特别地，对 $T(n)=c$ （ $c$ 为常数），称 $T(n)$ 在集合 $\Omega(1)$ 中。

如同“大欧”表示法一样，为了更加精确地描述，应当试图寻找最大的下限。

（三） “大西塔”表示法

如果一种算法既在 $O(h(n))$ 中，又在 $\Omega(h(n))$ 中，则称其为 $\Theta(h(n))$ （不再称在……中，因为上下限一致，不会再升阶或降阶）。实际上，如果能够给出一种算法在某种情况下的运行时间函数 $T(n)$ ，那么这种情况下，这种算法的上下限通常都是相等的。只有在不完全清楚待处理任务时，区别上限和下限才有意义。

排序问题的最差情况代价为 $\Theta(n\log n)$ 。

（四）化简法则

法则内容如下：

若 $f(n)$ 在 $O(g(n))$ 中，且 $g(n)$ 在 $O(h(n))$ 中，则 $f(n)$ 在 $O(h(n))$ 中；

若 $f(n)$ 在 $O(kg(n))$ 中，对于任意常数 $k>0$ 成立，则 $f(n)$ 在 $O(g(n))$ 中；

若 $f_1(n)$ 在 $O(g_1(n))$ 中，且 $f_2(n)$ 在 $O(g_2(n))$ 中，则 $f_1(n)+f_2(n)$ 在 $O(max(g_1(n),g_2(n)))$ 中；

若 $f_1(n)$ 在 $O(g_1(n))$ 中，且 $f_2(n)$ 在 $O(g_2(n))$ 中，则 $f_1(n)f_2(n)$ 在 $O(g_1(n)g_2(n))$ 中。

以上结论对大 $\Omega$ 表示法和大 $\Theta$ 表示法也成立。

法则1表示，如果 $g(n)$ 是 $f(n)$ 的上限，那么 $g(n)$ 的上限也是 $f(n)$ 的上限。
法则2表示，常数因子可被忽略。
法则3表示，对于顺序的两组语句或两段代码，只需考虑开销较大的部分。
法则4表示，对于一个有限次的循环而言，如果每一次循环的内容的开销相等，那么总开销就是每次的开销与重复次数之积。

（五）在增长率比较中的应用

对于给定的函数 $f(n)$ 和 $g(n)$ ，如果

$\lim\limits_{x\to \infty} \frac{f(n)}{g(n)}$

值趋向 $\infty$ ，则 $f(n)$ 在 $\Omega(g(n))$ 中；
值趋向0，则 $f(n)$ 在 $O(g(n))$ 中；
值趋向非0常数，则 $f(n)=\Theta(g(n))$ 。

五空间代价

空间代价是相对于数据结构而言的。渐进分析中增长率的概念对于空间代价同样适用。

对于一维数组而言，它的空间代价是 $\Theta(n)$ ；
对于二维数组而言，它的空间代价是 $\Theta(n^2)$ 。

一些术语：

结构性开销-并非真正数据的附加信息。例如链表中每个元素的指针。理论上，这种结构性开销应当尽可能小，但访问路径应该尽可能多而有效，二者之间需要权衡。
基于内存的时间/空间权衡原则-牺牲存储空间来减少时间代价或牺牲时间来减少空间代价。
基于磁盘（外存文件）的时间/空间权衡原则-由于从磁盘上读取数据的时间开销往往大于用于计算的时间开销，因此总是减少存储开销来减少时间代价（但并不总是这样）。

术语中反复提到权衡二字，这引导我们在设计程序时应当同时关注所权衡的二者的利害关系，试图寻找最适合实际情况的办法。

最后忠告：
先调整算法，后调整代码！

一 运行时间代价

二 增长率

三 最佳、最差和平均情况

四 渐进分析

（一） 上限——“大欧”表示法

（二） 下限——“大欧米伽”表示法