数据结构 | 内排序：Shell排序、归并排序和快速排序

一　Shell排序

  Shell排序试图将待排序序列变成基本有序的，然后利用插入排序来完成最后的排序工作。具体来说，它把序列分成多个子序列，然后分别对子序列进行排序，最后把子序列组合起来。
  下面是从教材中摘录的Shell排序的实现。这里的增量incr序列是$(2^k,2^{k-1},\cdots,2,1)$。

// Shell sort implementation
// Modified version of Insertion Sort for varying increments
template <typename E, typename Comp>
void inssort2(E A[], int n, int incr) {
  for (int i=incr; i<n; i+=incr)
    for (int j=i; (j>=incr) &&
                  (Comp::prior(A[j], A[j-incr])); j-=incr)
      swap(A, j, j-incr);
}

template <typename E, typename Comp>
void shellsort(E A[], int n) { // Shellsort
  for (int i=n/2; i>2; i/=2)      // For each increment
    for (int j=0; j<i; j++)       // Sort each sublist
      inssort2<E,Comp>(&A[j], n-j, i);
  inssort2<E,Comp>(A, n, 1);
}

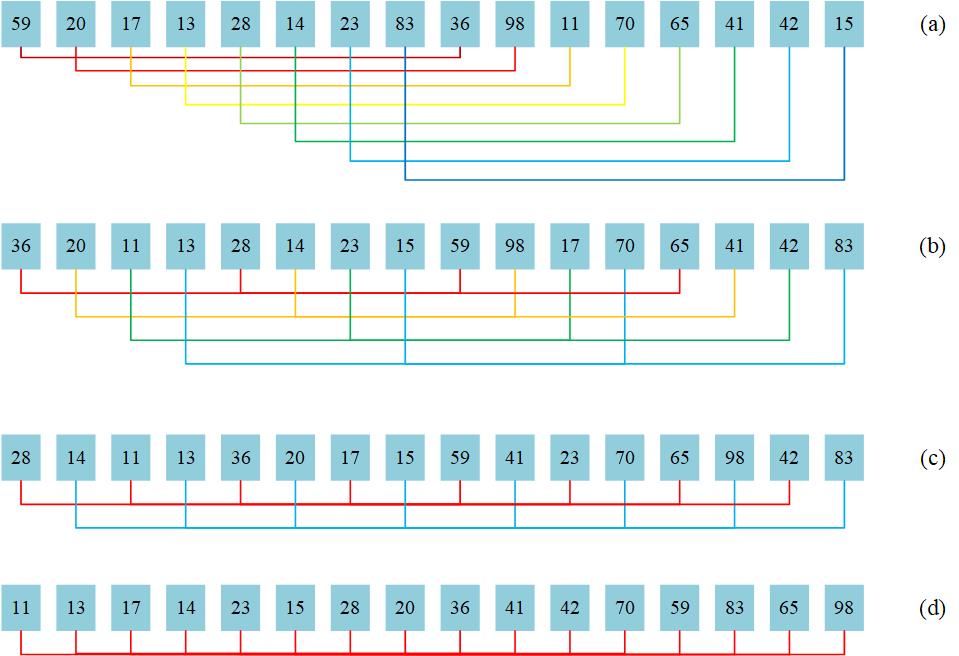
  现在通过一个示例进一步了解这个过程。对如图F1.a所示的序列执行如上代码所示的Shell排序，过程如下：

• 将序列划分为$\frac{n}{2}=\frac{16}{2}=8$个长度为2的的子序列，并且每一个子序列的元素下标相差8。然后在各个子序列内部执行插入排序，结果如图F1.b所示。
• 按照外层for循环的规则，当进行下一次循环时，有i/=2，此时将序列划分为$\frac{8}{2}=4$个长度为4的的子序列，并且每一个子序列的元素下标相差4。然后在各个子序列内部执行插入排序，结果如图F1.c所示。
• 继续执行，此时将序列划分为$\frac{4}{2}=2$个长度为8的的子序列，并且每一个子序列的元素下标相差2。然后在各个子序列内部执行插入排序，结果如图F1.d所示。
• 然后对现在的序列执行inssort2<E,Comp>(A, n, 1)，即完整的一次插入排序，就可以得到最终的结果。（因此增量序列的最后一位一定是1）

  Shell排序实际上是利用了插入排序在数组比较有序的情况下效率非常高的优点（注意到插入排序在最佳情况下的运行时间是$\Theta(n)$）。每一次外层循环，实际上都是将序列逐渐有序化的过程。更进一步地，对比进行一次插入排序和进行一次Shell排序，后者将序列划分为子序列来进行小型的插入排序。

Shell排序的时间复杂度：
  影响Shell排序的平均运行时间的因素之一是增量incr序列。有研究结果表明，在“增量每次除以3”的序列中，选择序列$(\cdots,121,40,13,4,1)$时效果更好，此时Shell排序的平均运行时间是$\Theta(n^{1.5})$。
  综合大量研究结果，Shell排序的平均运行时间一般认为介于$\Theta(n^{1.5})$和$\Theta(n^2)$之间。但这只是一个暂时的结果，有关Shell排序的增量序列的研究仍然是一个活跃的领域。

---

二　归并排序

  归并排序利用分治思想，递归地将待排序数组分为两部分，对每一部分进行排序，然后再将结果归并。
  下面是从教材中摘录的归并排序的实现。

// Basic mergesort implementation
template <typename E, typename Comp>
void mergesort(E A[], E temp[], int left, int right) {
  if (left == right) return;        // List of one element
  int mid = (left+right)/2;
  mergesort<E,Comp>(A, temp, left, mid);
  mergesort<E,Comp>(A, temp, mid+1, right);
  for (int i=left; i<=right; i++)   // Copy subarray to temp
    temp[i] = A[i];
  // Do the merge operation back to A
  int i1 = left; int i2 = mid + 1;
  for (int curr=left; curr<=right; curr++) {
    if (i1 == mid+1)      // Left sublist exhausted
      A[curr] = temp[i2++];
    else if (i2 > right)  // Right sublist exhausted
      A[curr] = temp[i1++];
    else if (Comp::prior(temp[i1], temp[i2]))
      A[curr] = temp[i1++];
    else A[curr] = temp[i2++];
  }
}

  现在阐释归并排序的过程：

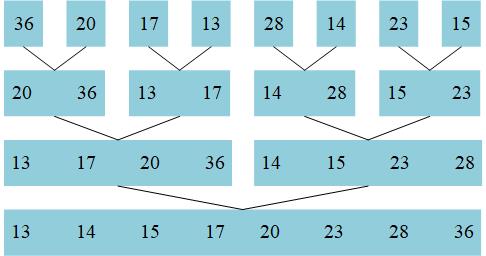
• 采用分治思想，归并排序首先有一段递归代码，每一次递归时，都计算int mid = (left+right)/2，将序列划分为两个子序列，其一从left到mid，其二从mid+1到right，分别进行排序。结束条件是if (left == right)，也就是划分到一个子序列只有一个元素，如图F2所示。
  

• 通过mergesort<E,Comp>(A, temp, left, mid); mergesort<E,Comp>(A, temp, mid+1, right);得到左右子序列已经完成排序的序列。

• 将序列复制到temp数组中备用。

• int i1 = left;记录左子序列的初始位置，int i2 = mid + 1;记录右子序列的初始位置。

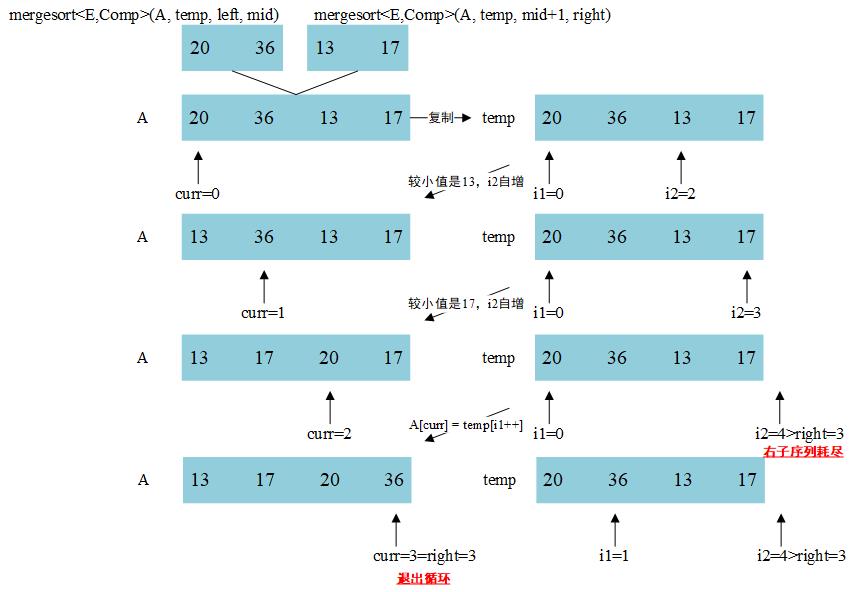
• 使用for循环对序列遍历，对原数组A进行更新。首先利用Comp::prior(temp[i1], temp[i2])比较左右子序列的第一个元素，如果temp[i1]较小，则将当前位置A[curr]设置为temp[i1]，然后将i1自增（注意i1++表示先使用i1再自增）；反之将当前位置A[curr]设置为temp[i2]，然后将i2自增，直至左右子序列中有一方已经完全耗尽。如果左子序列耗尽，那么原数组中剩余部分只需要按照右子序列的剩余部分填充；反之亦然。以图F2的其中一步为例，图F3形象地展示了这个过程。

  教材还给出了一种优化办法来精简上述流程。在这种方法中，将序列复制到temp数组时将右子序列的顺序颠倒，比较与归并过程从两端开始向中间推进，使得这两个子数组的两端互相成为另一个数组的“监视哨”。这样一来，就不必检查左右子序列是否耗尽。同时，当划分的子序列较短时，改用插入排序处理。
  下面是从教材中摘录的归并排序的优化实现。

//Optimized mergesort implementation
template <typename E, typename Comp>
void mergesort(E A[], E temp[], int left, int right) {
  if ((right-left) <= THRESHOLD) { // Small list
    inssort<E,Comp>(&A[left], right-left+1);
    return;
  }
  int i, j, k, mid = (left+right)/2;
  mergesort<E,Comp>(A, temp, left, mid);
  mergesort<E,Comp>(A, temp, mid+1, right);
  // Do the merge operation.  First, copy 2 halves to temp.
  for (i=mid; i>=left; i--) temp[i] = A[i];
  for (j=1; j<=right-mid; j++) temp[right-j+1] = A[j+mid];
  // Merge sublists back to A
  for (i=left,j=right,k=left; k<=right; k++)
    if (Comp::prior(temp[i], temp[j])) A[k] = temp[i++];
    else A[k] = temp[j--];
}

  其中THRESHOLD是一个用户自定义的常量，表示用户可以接受的、使用插入排序的数组长度。最后一个for循环中，i和j以temp数组的最左端（左子序列的最小值）、最右端（由于颠倒排序，这里是右子序列的最小值）开始依次比较，并将A[k]设置为其中的较小值，然后被设置的一方完成自增（对于i）或自减（对于j）工作，最后k自增，进入下一轮循环。

归并排序的时间复杂度：
  通过以上的分析可以知道，归并过程实质上是将元素一一填入原数组的过程，因此对于每一次归并而言，假设该次归并结果的总长为i，那么该次归并需要花费$\Theta(i)$的时间。对于一个总长为n（为简单起见，假设n是2的幂）的数组，递归一共有$\log n+1$层（比如对图F2而言，长度为8的序列递归一共有4层）。对于每一层而言，比如对图F2，第一层是1个长度为8的数组的排序，第二层是2个长度为4的数组的排序，第三层是4个长度为2的数组的排序，第四层是8个长度为1的数组的排序，如果推广开来，就是：

• 第一层是1个长度为$n$的数组的排序，需要$1 \times \Theta(n)=\Theta(n)$的时间；
• 第二层是2个长度为$n/2$的数组的排序，需要$2 \times \Theta(n/2)=\Theta(n)$的时间；
• 第三层是4个长度为$n/4$的数组的排序，需要$4 \times \Theta(n/4)=\Theta(n)$的时间；
• $\cdots$
• 最后一层是n个长度为1的数组的排序，需要$n \times \Theta(1)=\Theta(n)$的时间。

  因此，总时间代价为$(\log n+1) \times \Theta(n)=\Theta(n\log n)$（因为渐进分析相关原理，低阶项$n$被省略）。注意到在分析过程中，该时间代价与数值的相对顺序无关，因此它是归并排序的最佳、平均、最差运行时间。

---

三　快速排序

  快速排序选择一个轴值对序列进行划分，它以一种更为有效方式实现了“分治思想”。
  下面是从教材中摘录的快速排序的实现。

// qsort core function: Basic qsort
template <typename E, typename Comp>
void qsort(E A[], int i, int j) { // Quicksort
  if (j <= i) return; // Don't sort 0 or 1 element
  int pivotindex = findpivot(A, i, j);
  swap(A, pivotindex, j);    // Put pivot at end
  // k will be the first position in the right subarray
  int k = partition<E,Comp>(A, i-1, j, A[j]);
  swap(A, k, j);             // Put pivot in place
  qsort<E,Comp>(A, i, k-1);
  qsort<E,Comp>(A, k+1, j);
}

  其中，i j是待排子序列左右两端的下标。和归并排序相同的是，快速排序也是一个递归过程。
  现在来对这个流程做分析：

• 递归的终止条件是if (j <= i)，即子序列中的元素个数是0或1。
• 函数findpivot寻找并返回轴值的下标。下面是从教材中摘录的一种简单的findpivot函数，它选取数组中间点作为轴值。注意，根据对序列元素分布的了解程度的不同，该函数的实现策略也会有所不同。

// Simple findpivot: Pick middle value in array
template <typename E>
inline int findpivot(E A[], int i, int j)
  { return (i+j)/2; }

• 利用swap(A, pivotindex, j)将轴值与最后一个元素做交换，然后利用函数partition来分割序列，使左端的值都小于轴值，右端的值都大于轴值。下面是从教材中摘录的partition函数。它从数组两段移动下标，必要时交换记录，直到数组两端的下标相遇为止。

// Partition the array
template <typename E, typename Comp>
inline int partition(E A[], int l, int r, E& pivot) {
  do {             // Move the bounds inward until they meet
    while (Comp::prior(A[++l], pivot));  // Move l right and
    while ((l < r) && Comp::prior(pivot, A[--r])); // r left
    swap(A, l, r);              // Swap out-of-place values
  } while (l < r);              // Stop when they cross
  return l;      // Return first position in right partition
}

  有一些细节需要注意。在快速排序的实现中，分割语句是int k = partition<E,Comp>(A, i-1, j, A[j]);也就是说左端下标是i-1，右端下标是j。在进入函数partition的do循环后：

• 第一个while循环从左向右寻找大于轴值的值，准备做交换，注意到其中++l先自增后使用，因此实际上是从位置i开始寻找；
• 第二个while循环从右向左寻找小于轴值的值，准备做交换，注意到其中--r先自减后使用，因此实际上是从位置j-1开始寻找，直至l >= r，即下标相遇，这个时候的下标所指引的值是从右向左大于轴值的最后一个值，也是该函数的返回值。为什么是从位置j-1开始寻找呢？这是因为在int k = partition<E,Comp>(A, i-1, j, A[j]);之前的swap(A, pivotindex, j)语句将轴值交换到了序列的最后一个，它并不需要参与序列分割。

• 利用swap(A, k, j);来交换轴值和从右向左大于轴值的最后一个值，得到的序列就以轴值为界限，左端小于之，右端大于之。
• 现在的序列中轴值左端的值和轴值右端的值还没有完成排序，继续利用qsort<E,Comp>(A, i, k-1); qsort<E,Comp>(A, k+1, j);对子序列应用快速排序（轴值不参与）。

快速排序的时间复杂度：
  依次分析各个函数所消耗的时间。显然函数swap和findpivot都消耗常数时间。比较复杂的是函数partition。do循环每执行一次，l和r都向前移动至少一步（除非下标相遇，否则自增一定会发生，并且下标相遇只会发生一次）。因此对于一个长度为s的数组，do循环最多执行s次（每次do循环l和r都向前移动一步），其中嵌套的两个while循环（一个控制l移动，另一个控制r移动）在每一次do循环中执行至少一次，于是partition函数的时间代价是$\Theta(s)$。
  基于以上结论，现在来分析快速排序的时间代价：

• 最差情况下，轴值并没有很好地划分序列。对于一个长度为s的序列来说，划分后一个子序列中没有元素，另一个子序列中有s-1个元素（轴值不参与）。那么对总长为n的序列，在整个过程中，依次要对包含$n,n-1,\cdots,1$个元素的序列执行快速排序（有一个细节是，对1个元素执行快速排序时，会因为递归终止条件立即返回）。这样一来在最差情况下，整个排序过程的总时间代价是$\sum\limits_{k=2}^{n}k=\Theta(n^2)$。
• 最佳情况下，轴值将序列等分。此时对总长为n的序列，一共需要递归$\log n$次，每一次递归，将序列分别划分为2个$n/2$的序列、4个$n/4$的序列、8个$n/8$的序列，以此类推。每一次递归的序列总长都为n，因此每一次递归的时间代价是$\Theta(n)$。因此在最佳情况下，整个排序过程的总时间代价是$\Theta(n\log n)$。
• 平均情况下，假设每一次划分时，轴值的位置是等可能性的，也就是说将一个长度为s的序列分为0和s-1，1和s-2，2和s-3等等的概率是相等的。那么就有

$$T(n)=cn+\frac{1}{n}\sum\limits_{k=0}^{n-1}[T(k)+T(n-1-k)]$$

其中，$T(0)=T(1)=c$，$cn$表示花费常数时间的函数所消耗的时间，$\frac{1}{n}$表示不同分割方式的概率相等（显然对长度为n的序列，在区分左右的情况下，一共有n种分割方式），$T(k)+T(n-1-k)$表示对左右子序列进行快速排序所消耗的时间。因此在平均情况下，整个排序过程的总时间代价是$\Theta(n\log n)$。

一些拓展的信息：
  快速排序算法的运行时间是可以改进的。

• 轴值：
    在众多研究中，最明显的可改进之处与函数findpivot有关，这是因为轴值能否很好地划分序列对整个排序过程有着重要影响。例如使用“三者取中法”选取序列中第一个、中间一个和最后一个数值的中间大小的一个作为轴值，在实现简单的同时往往比固定地选取第一个/中间一个/最后一个值作为轴值表现出更好的性能。
• 短数组：
    事实上，当数组长度较小时，快速排序也比较慢。经验表明，最好的方式是当数组长度被划分至小于或等于9时改用插入排序。
• 递归调用：
    由于每个快速排序操作都需要对两个子序列进行排序，因此没有简单的方法将递归转换成等价的循环算法。但是，当存储的信息不多时，可以使用栈来模拟递归调用。同时，也无需存储子序列的部分，而改为保存其边界。也可以将函数findpivot和函数partition变为直接编码形式嵌入算法中。这样，不处理长度为9（甚至更短）的子序列时，就能消除75%的函数调用。