数据结构 | 内排序：堆排序、分配排序和基数排序

一　堆排序

堆排序基于堆的数据结构。以最大堆为例，下面是从教材中摘录的堆排序的实现。

// Standard heapsort implementation
template <typename E, typename Comp>
void heapsort(E A[], int n) { // Heapsort
  E maxval;
  heap<E,Comp> H(A, n, n);    // Build the heap
  for (int i=0; i<n; i++)        // Now sort
    maxval = H.removefirst();    // Place maxval at end
}

分析这个for循环，对于n个元素的最大堆，函数removefirst将最大值置于下标n-1的位置，然后最大堆减少1个元素；然后对于n-1个元素的最大堆，函数removefirst将最大值置于下标n-2的位置，然后最大堆减少1个元素,。以此类推。最终就得到了由小到大排列的数组。

堆排序的时间复杂度：
根据对堆的分析：

建堆过程的时间代价是 $\Theta(n)$ ；
for循环完成n次取最大元素的操作(也就是将根结点依次移至数组末尾），每一次循环需要 $\Theta(\log n)$ 的时间，请注意，由于堆不断减小，所以整个for循环消耗的时间应该是
$\sum\limits_{i=1}^{n}=\Theta(\log i)=\Theta(\log n!)$
近似为 $\Theta(n\log n)$ 。

因此，应用化简法则，堆排序在最佳、平均、最差情况下的时间代价是 $\Theta(n\log n)$ 。尽管堆排序一般情况下要比快速排序在常数因子上慢，但它有独特的优势——如果需要找到第k大的元素，可以用 $\Theta(n+k\log n)$ 的时间（如果k很小，这将是一个巨大的优势）。

二　分配排序

分配排序的基本思想是将序列经过一次遍历后分类，然后对每一类别排序，此时每一类别的数量很少。
下面是从教材中摘录的分配排序一个最基本例子的实现。

1 2	for (i=0; i<n; i++) B[A[i]] = A[i]

这个例子用来对0到n-1的序列进行排序，并且显然它只需要 $\Theta(n)$ 的时间代价。以数组B的每一个位置为一个类别，这个遍历过程将数组A的每一个元素分类至类别中，完成排序。
这种思想在关键码值允许重复时更加明显，此时被分类到数组B的某一个位置的元素不止一个。将数组的每一个位置改为链表，下面是从教材中摘录的分配排序一个拓展例子的实现。

template <typename E, class getKey>
void binsort(E A[], int n) {
  List<E> B[MaxKeyValue];
  E item;
  for (int i=0; i<n; i++) B[A[i]].append(getKey::key(A[i]));
  for (int i=0; i<MaxKeyValue; i++)
    for (B[i].setStart(); B[i].getValue(item); B[i].next())
      output(item);
}

这个例子用来对0到MaxKeyValue-1的序列进行排序，并且当MaxKeyValue比n小时，它只需要 $\Theta(n)$ 的时间代价。然而当MaxKeyValue比n大时，例如MaxKeyValue为 $n^2$ ，此时它需要 $\Theta(n+n^2)=\Theta(n^2)$ 的时间代价，当相差更大时，情况更糟糕。
分配排序的进一步拓展是桶式排序。此时，数组B的某一个位置（称为“桶”）并非只与一个关键码值关联，而是与一个范围内的关键码值关联。这种排序方式把记录放到“桶”中，然后借助于其他排序技术对“桶”中的记录进行排序。

三　基数排序

基数排序基于关键码的某个位来分配盒子。当基数为10时，基数排序从最右边的位（个位）开始，到最左边的位（最高位）为止，每次按照关键码的某位数字把它分配到盒子中。如果关键码有k位数，就需要进行k次分配。
下面是从教材中摘录的基数排序的实现。

// Radix sort implementation
template <typename E, typename getKey>
void radix(E A[], E B[],
           int n, int k, int r, int cnt[]) {
  // cnt[i] stores number of records in bin[i]
  int j;

  for (int i=0, rtoi=1; i<k; i++, rtoi*=r) { // For k digits
    for (j=0; j<r; j++) cnt[j] = 0;        // Initialize cnt

    // Count the number of records for each bin on this pass
    for (j=0; j<n; j++) cnt[(getKey::key(A[j])/rtoi)%r]++;

    // Index B: cnt[j] will be index for last slot of bin j.
    for (j=1; j<r; j++) cnt[j] = cnt[j-1] + cnt[j];

    // Put records into bins, work from bottom of each bin.
    // Since bins fill from bottom, j counts downwards
    for (j=n-1; j>=0; j--)
      B[--cnt[(getKey::key(A[j])/rtoi)%r]] = A[j];

    for (j=0; j<n; j++) A[j] = B[j];    // Copy B back to A
  }
}

现在来分析这个过程：

k指示所排序关键码的最大位数。外层for循环执行k次分配。
cnt数组开辟了一块空间，用来存储放到每一个盒子的记录数目。内部的第一个for循环对该数组进行初始化。
第二个for循环计算要放到每个盒子的记录数。其中，数组A存储待排序的记录，方法key用来获取这些记录的关键码值，变量rtoi是基数的幂，变量r是基数（即盒子的数量）。在这个for循环中，首先获取关键码值，然后除以基数的幂，再对基数取模，这就得到了盒子的位置。随后在cnt数组中，对这个位置的数目加1，遍历完所有记录后，这个数组中就存储了放到每个盒子的记录数。
例如当基数是10时，在外层循环进行两次以后，rtoi=100，这时对于关键码值1234，就有1234/100=12，然后12%10=2，得到应该将1234放在下标为2的盒子中，因此计数cnt[2]加1。
第三个for循环计算每一个记录应该放在数组B中的下标（加1）。
第四个for循环将数组A中的记录按照顺序放入数组B中暂存。注意每一次放入前，都会执行自减操作。这是由于数组cnt中存储的是个数（或个数的和），比如cnt[]=[2,5,6]，这意味着放入第一个盒子的有两个元素，那么放入数组B中时就应该依次置于下标为1和0的位置（注意这个循环是自后向前的，如果从前往后，以上逻辑将会更复杂）。
第五个for循环将数组B拷贝回数组A作为排序结果。

图F1列举了一个基数排序的示例，形象地说明了上述过程。
F1.基数排序示例

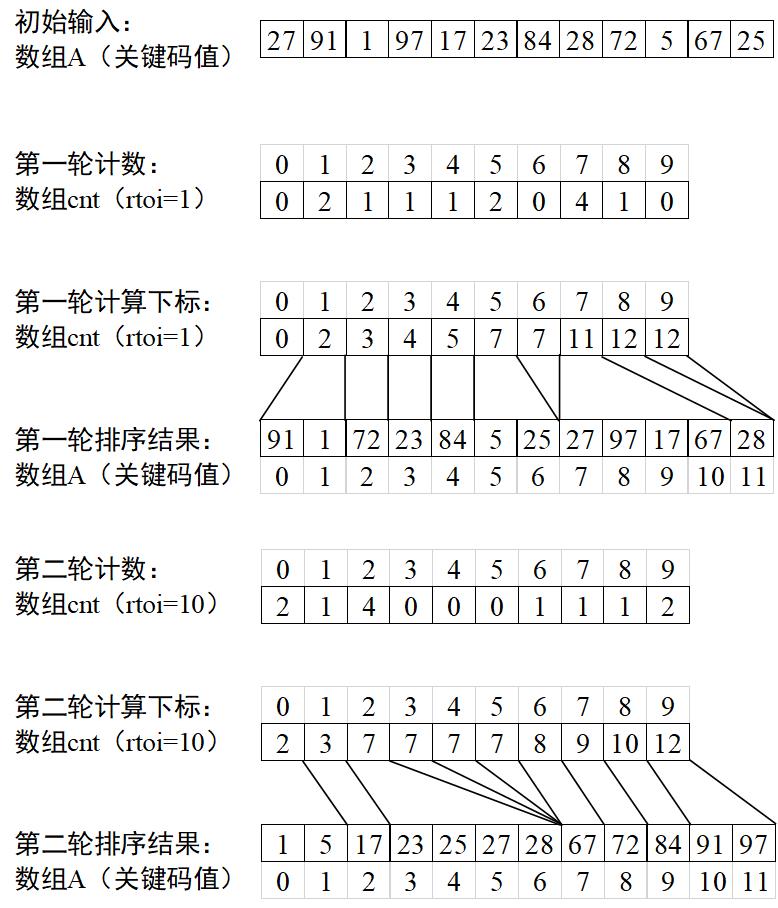
基数排序的时间复杂度：
对于n个数据的序列，假设基数为r，分配次数是k，那么观察代码中的for循环，每一轮分配的时间就是 $\Theta(3n+2r)=\Theta(n+r)$ ，因此总时间代价是 $\Theta(nk+rk)$ 。基数r根据需要来变动，例如一般来说，对十进制数排序使用基数10，对二进制数排序用基数2，对只含字母的（不区分大小写）字符串排序使用基数26。在分析时间复杂度时，将基数r视作常数，忽视它的影响。同时，变量k与关键码的长度有关，它是以r为基数时，关键码可能拥有的最大位数，可以认为k是有限的。在分析时间复杂度时，将变量k视作常数，忽视它的影响。
这样的假设之下，基数排序的最佳、平均、最差时间代价是 $\Theta(n)$ 。
如果关键码不允许重复，则 $k \leq \log_rn$ 。此时，至少需要 $\Omega (\log n)$ 位来区分关键码值，那么k在 $\Omega (\log n)$ 中，因此，在这种假设下需要花费 $\Omega (n\log n)$ 的时间代价。

一些拓展的信息：
基数排序算法的运行时间可以通过变化基数改进。
基数r应当尽量大些。例如对于整型关键码而言，令 $r=2^i$ ，其中i是某个表示处理位数的整数。可以注意到r的大小与i有关。如果i增加一倍，则分配的轮次可以减少一半。例如处理整形关键码时，令 $r=2^8$ ，则一轮分配可以处理8个二进制位，那么处理一个32位的关键码需要4轮分配；令 $r=2^{16}$ ，则一轮分配可以处理16个二进制位，那么处理一个32位的关键码需要2轮分配.

一 堆排序

二 分配排序

三 基数排序

一　堆排序

二　分配排序

三　基数排序